RESEARCH

Our research focuses on understanding the fundamental properties of quantum chromodynamics (QCD), the theory of the strong interaction, under extreme conditions of temperature, density, and magnetic fields. Using state-of-the-art lattice QCD simulations, we explore the thermodynamics of strongly interacting matter, the QCD phase structure, and the properties of the quark-gluon plasma (QGP). These studies are crucial for interpreting phenomena in heavy-ion collisions, the early universe, and compact astrophysical objects like neutron stars. 

A central theme of our work is the investigation of chiral symmetry breaking and restoration, the QCD critical endpoint, and axial U(1) anomaly in high-temperature and dense environments. We are also interested in mesonic excitations, transport properties, and the interplay between QCD dynamics and external magnetic fields.

1. Chiral Symmetry Breaking and Restoration

Chiral symmetry is a fundamental property of quantum chromodynamics (QCD), the theory of the strong interaction. In the vacuum, chiral symmetry is spontaneously broken, a phenomenon responsible for the generation of hadron masses and the emergence of pions as pseudo-Nambu-Goldstone bosons. This breaking of chiral symmetry is a key feature of low-energy QCD and plays a central role in shaping the hadronic spectrum. 

At high temperatures or densities, such as those created in heavy-ion collisions or present in the early universe, chiral symmetry is expected to be restored. This restoration marks a transition from a phase where quarks and gluons are confined into hadrons to a deconfined phase known as the quark-gluon plasma (QGP). The study of this chiral phase transition is crucial for understanding the QCD phase diagram and the behavior of strongly interacting matter under extreme conditions. 

The nature of the chiral phase transition depends on the number of quark flavors and their masses. For massless quarks, the transition is expected to be a true phase transition, while for physical quark masses, it becomes a smooth crossover. A key question in this context is the identification of the QCD critical endpoint, a hypothetical point in the phase diagram where the crossover transitions into a first-order phase transition at finite density. 

Chiral symmetry restoration is also closely connected to the axial U(1) anomaly, which explicitly breaks the axial symmetry of QCD. The interplay between chiral symmetry restoration and the axial anomaly has significant implications for the phase structure of QCD, including the behavior of mesonic excitations and the thermodynamics of the QGP. 

Understanding chiral symmetry breaking and restoration is not only essential for mapping out the QCD phase diagram but also for interpreting phenomena in heavy-ion collisions, neutron stars, and the early universe. These studies provide deep insights into the fundamental properties of strongly interacting matter and the dynamics of QCD across different energy scales. 

Representative publications include:

2. Interplay of QCD Dynamics with Magnetic Fields

The behavior of quantum chromodynamics (QCD) in strong external magnetic fields is a fascinating area of research that bridges fundamental theory, heavy-ion collision experiments, and astrophysics. Strong magnetic fields, generated in off-central heavy-ion collisions or present in neutron stars, provide a unique probe of the non-perturbative structure of QCD and its interplay with electromagnetic phenomena.

At a fundamental level, the coupling of QCD dynamics to magnetic fields is deeply connected to the axial U(1) anomaly, a key feature of QCD that breaks the classical conservation of axial charge. This anomaly arises from topological fluctuations in the gluon fields and has profound implications for the phase structure of QCD, the spectrum of mesonic excitations, and the thermodynamics of strongly interacting matter. In the presence of a magnetic field, the axial anomaly can lead to novel transport phenomena and modify the properties of the quark-gluon plasma (QGP).

One striking consequence is the potential emergence of chiral imbalance in systems subject to strong magnetic fields. This imbalance, driven by the axial anomaly, can influence the QCD phase diagram, particularly near the chiral phase transition. Magnetic fields enhance chiral symmetry breaking at low temperatures and affect its restoration at high temperatures, offering insights into the nature of the QGP.

In heavy-ion collisions, the transient but intense magnetic fields generated in off-central collisions provide a laboratory for studying these effects. The interaction of quarks and gluons with these fields can lead to observable signatures in the collective behavior of the produced matter, shedding light on the topological structure of QCD.

Beyond heavy-ion collisions, the interplay of QCD dynamics with magnetic fields is crucial for understanding neutron stars. Strong magnetic fields can influence the equation of state, the formation of exotic phases of matter, and transport properties, leaving observable imprints on the star’s cooling and rotational dynamics.

By exploring this interplay, we aim to deepen our understanding of strongly interacting matter under extreme conditions, connecting fundamental QCD physics to phenomena in heavy-ion collisions and astrophysics.

Representative publications include:

3. QCD at nonzero baryon density

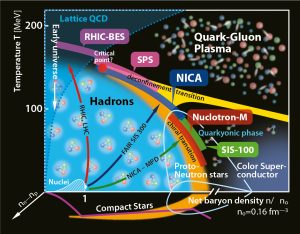
The study of quantum chromodynamics (QCD) at nonzero baryon density is essential for understanding the phase structure of strongly interacting matter under extreme conditions, such as those in heavy-ion collisions and neutron stars. A central goal of this research is the search for the QCD critical endpoint, a hypothetical point in the phase diagram where the smooth crossover between hadronic matter and the quark-gluon plasma (QGP) transitions into a first-order phase transition. The existence and location of this critical endpoint are often referred to as a “holy grail” in the study of QCD phase structure, as its discovery would provide profound insights into the nature of strongly interacting matter.

Lattice QCD, a first-principles numerical approach, has been highly successful in studying QCD at zero or low baryon densities, offering precise results for the QGP and the crossover region. However, extending these calculations to higher baryon densities is severely hindered by the sign problem, a fundamental challenge arising from the complex nature of the QCD action at finite chemical potential. This problem makes traditional lattice QCD methods impractical for exploring the high-density regime, where the critical endpoint is expected to lie.

To address this challenge, lattice QCD researchers have developed and refined a variety of techniques over the years, including Taylor expansions around zero density, and simulations at imaginary chemical potential, Comlpex Langevin equation etc. These approaches have provided valuable constraints on the QCD phase diagram and the possible location of the critical endpoint, even if they cannot yet fully overcome the limitations imposed by the sign problem.

Heavy-ion collision experiments are at the forefront of the search for the critical endpoint, probing the high-density regime by varying collision energies and measuring observables sensitive to critical fluctuations. These experiments provide essential data that complement theoretical efforts, helping to narrow down the location of the critical endpoint and test predictions from lattice QCD and other theoretical approaches.

With lattice QCD, we aim to push the boundaries of our understanding by developing new methods to tackle the sign problem, refining calculations of the QCD phase diagram, and providing precise theoretical inputs to guide experimental searches for the critical endpoint. By combining these efforts, we strive to uncover the fundamental properties of strongly interacting matter at nonzero baryon density and deepen our understanding of QCD under extreme conditions.

Representative publications include:

Our group also explores the structure of hadrons, focusing on generalized parton distributions (GPDs), electromagnetic form factors etc. We aslo aim to develop and apply advanced numerical algorithms and leverage large-scale supercomputing facilities.